Flattening Examples
Here are a few examples to give people an idea of what the flattening process for generalized arrows looks like in real life. Dashed lines represent inputs and outputs whose type is the unit of the generalized arrow (roughly analogous to () in Haskell). The GHC pass that performs the translation is written in Coq, and is formally proven to be type-correct: the result of the flattening process is always a well-typed term whose type is derived in a predictable way from the type of the term and the types of its free variables. If you compile this file:
{-# OPTIONS_GHC -XModalTypes -fflatten -funsafe-skolemize -dcore-lint #-}
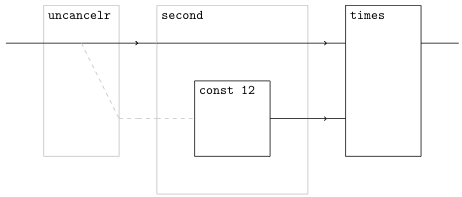
module Demo (demo) where demo const times = <[ \y -> ~~times y ~~(const 12) ]> You get this diagram:
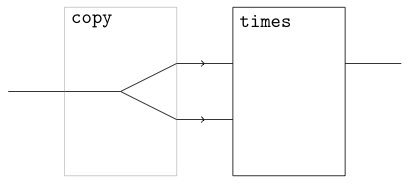
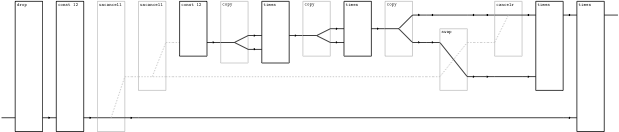
To see how fanout works, try this program:
{-# OPTIONS_GHC -XModalTypes -fflatten -funsafe-skolemize -dcore-lint #-}
module Demo (demo) where demo const times = <[ \y -> ~~times y y ]>
Which gives you this diagram (full
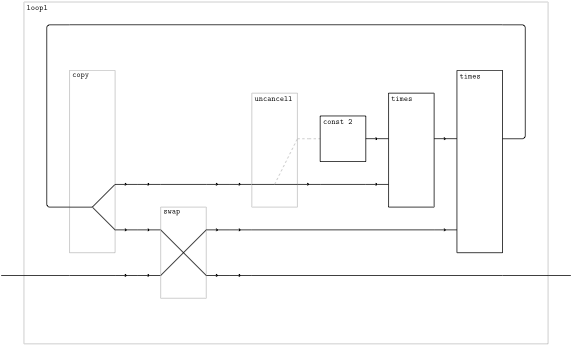
To see how feedback works, try this program:
{-# OPTIONS_GHC -XModalTypes -fflatten -funsafe-skolemize -dcore-lint #-}
module Demo (demo) where demo const times = <[ \x -> let out = ~~times (~~times ~~(const 2) out) x in out ]> Which gives you this diagram:
The image above is rendered in a mode which omits ga_first, ga_second, ga_assoc, and ga_unassoc. You can find the “verbose” diagram, which includes these elements, The example above involves recursion inside the brackets, which is flattened into diagrams with feedback. The example below shows how recursion outside the brackets is used to produce repetitive structures:
{-# OPTIONS_GHC -XModalTypes -fflatten -funsafe-skolemize -dcore-lint #-}
module Demo (demo) where demo const times = <[ \y -> ~~(pow 9 12) ]> where -- "pow n x" computes x^n pow 0 x = const (1::Int) pow 1 x = const x pow n x = <[ ~~times ~~(pow 1 x) ~~(pow (n-1) x) ]>
Which gives you the diagram below (full
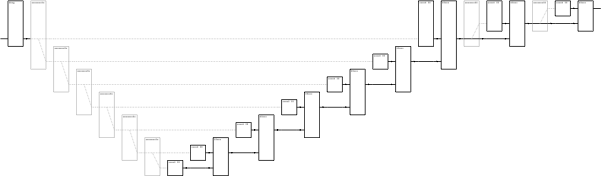
The program above produces a diagram whose size is linear in the value of the exponent. Here is a more efficient program which produces a diagram with size logarithmic in the value of the exponent:
{-# OPTIONS_GHC -XModalTypes -fflatten -funsafe-skolemize -dcore-lint #-}
module Demo (demo) where demo const times = <[ \y -> ~~(pow 9 12) ]> where -- "pow n x" computes x^n pow 0 x = const (1::Int) pow 1 x = const x pow n x | n `mod` 2 == 0 = <[ let x_to_n_over_2 = ~~(pow (n `div` 2) x) in ~~times x_to_n_over_2 x_to_n_over_2 ]> | otherwise = <[ ~~times ~~(pow (n-1) x) ~~(const x) ]>
Which gives you the diagram below (full
Implementation DetailsAll examples above come from modules compiled with -fflatten, the new GHC flag which enables the flattening pass on a module-at-a-time granularity. Functions in the flattened module are then called by a non-flattened module DemoMain which uses GArrowTikZ (which in turn uses TikZ, lp_solve, and pdflatex) to render them.
import GArrowTikZ
import Demo main = tikz demo You'll notice that these modules also use the flag -funsafe-skolemize. This enables a skolemization pass before flattening, which attempts to convert first-order functions (values of type t1->t2 where t1 is not a function) into let-bindings. If successful, the resulting generalized arrow term will not use ga_curry or ga_apply; this is important if you want to get “boxes and wires” diagrams, because ga_curry and ga_apply leave you with diagrams that don't yield a whole lot of insight. The -funsafe-skolemize flag has “unsafe” in its name because it is technically unsafe in the presence of certain kinds of polymorphism. Basically, if you have a type variable which appears in a code type, don't ever instantiate it with a type that is a function. The type system ought to check for this, but it currently does not. The -funsafe-skolemize flag automatically enables the -fflatten flag, which in turn automatically enables the -fcoqpass flag. If you use -fcoqpass by itself, GHC will simply convert the CoreSyn to HaskProof and back – this is used to check for bugs in the “glue code” that connects the Haskell world to the Coq world. Why Two Modules?This two-module form is the simplest way to deal with the fact that:
Prior to flattening, the combined program is not actually well-typed – it tries to pass a multi-level-typed term to a function expecting a GArrow term (try removing -fflatten and -funsafe-skolemize and see what happens). Therefore, we typecheck the modules separately, flatten one of them, and then link the results – by the time we get to linking the program as a whole is well-typed. InefficiencyYou'll notice there are quite a lot of extra dashed lines! I'm working on a more efficient coding. The flattener produces a “wire” for every free variable in the term and for each type in its uncurrying. For example, if the term is of a function type a->b->c->d its uncurrying is a*b*c->d and it would have three types. At the moment there are three serious inefficiencies:
Overall, it's often easier to prove a verbose translation correct than to prove a clever one correct – the induction hypotheses are simpler and have fewer cases. Since the “equational theory of the initial premonoidal category” is a rather simple theory (you can't encode anything like arithmetic in it) I strongly suspect that there is some sort of normal form criteria and a reasonably efficient normalization procedure. Evaluation OrderEvaluation is left-to-right; when turning a multi-level term into a generalized arrow term,
let x1 = e1
in x2 = e2 in e3 becomes (roughly)
ga_first [[e1]] >>> ga_second [[e2]] >>> [[e3]]
not
ga_second [[e2]] >>> ga_first [[e1]] >>> [[e3]]
However, there are two quirks:
I'm working on getting a better handle on these issues; I think they can all be eliminated.
|